

|
|
|
|
|
Nonlinear optical systems are a very useful context for the study of general nonlinear phenomena because of their versatility, easy experimental accessibility, time scales involved, and also for their relevance in applications in information technologies. Our line of research is within the general theoretical and computational study of spatial pattern formation in the plane transverse to the direction of beam propagation. Specific aspects of pattern formation in these systems are the diffractive coupling, the vectorial character of the light field and the existence of macroscopic manifestations of quantum correlations. We study Optical Parametric Oscillators (OPO) in which photons of frequency 2w are down converted in photons of frequency w in an optical cavity, and Kerr media (cubic nonlinear electric susceptibility).
|
|
The problem of domain growth and motion of domain walls has been studied in detail in the context of the Dynamics of Phase Transitions, where physical mechanisms, asymptotic power laws and self-similar evolution have been established. This problem is now being addressed in optical systems, where the dynamics does not minimize an equilibrium free energy and it is mostly non-dissipative. Domains can be here of different light intensity, phase, or polarization of the electric field. Dynamical evolution can also lead to localized structures or cavity solitons useful for parallel optical information processing.
|
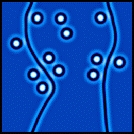
| We have studied the transient dynamics of the transverse spatial structures
in an optical cavity filled with a vectorial Kerr medium and pumped by
linearly polarized light. For large pump values equivalent homogenous domains
of opposite elliptical polarization emerge, separated by polarization domain
walls. We have shown that a curvature dominated asymptotic
growth law holds, and we have shown self-similar evolution for the first
time in an optical system. For smaller pump values the domain wall collapses
into a polarized localized structure. A modulational instability of the
domain wall for small pump values leads to labyrinthine frozen patterns.
R. Gallego, M. San Miguel and R. Toral, Physical Review E 61, 2241(2000). |
|
|
Different studies have predicted stationary intensity stripe patterns in OPOs, which have been recently observed experimentally by C. Fabre and collaborators (Phys. Rev. Lett. 83, 5278 (1999)). These devices are also good candidates for the study of quantum macroscopic phenomena because the basic process is twin photon emission. Not much was known for type-II OPO, where the two down converted photons are orthogonally polarized and walk-off from each other. We had shown in the past that walk-off generically leads to a convective regime, with macroscopic patterns sustained by quantum noise.
|
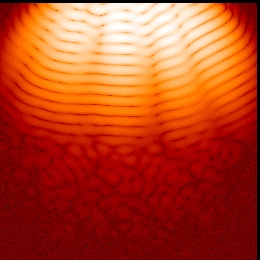
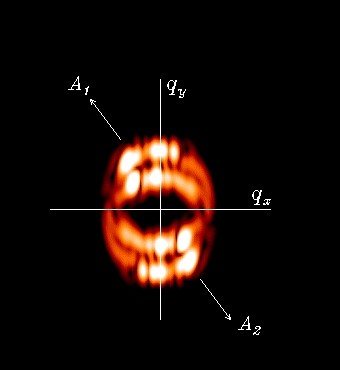
We have studied the relevance of walk-off effects
in pattern formation in a type-II OPO. We have found that:
There is a regime of absolutely instability for large pump values. In this regime there is a competition between two phase stripe patterns (travelling waves) of different wavelength for each polarization of the fundamental harmonic fields. The phase stripe patterns for each wavelengths are equally likely to be selected after a transient regime of coexistence and competition. For lower values of the pump there is a convectively unstable regime in which intensity patterns sustained by noise are observed for each polarization. This patterns arise from the interference among traveling waves that are generated by the dynamical amplification of noise. G. Izús, M. Santagiustina, M. San Miguel and P. Colet, J. Opt. Soc. Am. B 16, 1592 (1999) |
|
|
Nonlinear optical patterns display deep quantum aspects which arise essentially from the quantum entanglement or quantum correlation of the spatial modes that generate the pattern. These issues have been studied in OPOs, Kerr cavities, and in cavityless configurations for quadratic and cubic nonlinear media. However, in general , the vectorial character of the light has not been taken into account, despite the fact that in many cases it originates a much richer scenario of pattern forming instabilities. In particular for a self-defocusing Kerr cavity with linearly polarized pump, a stripe pattern orthogonally polarized to the pump is formed (M. Hoyuelos et al, Phys. Rev E, 58, 2992 (1998)) whereas no pattern formation occurs in the scalar case.
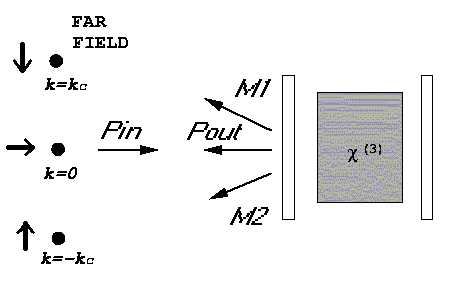
On the left box, the upper figure shows a diagram of the Kerr cavity. Pin is the input pump field . In addition to the outgoing signal Pout, the spatial instability generates two off-axial meter beams M1 and M2.The lower figures show the results for the self-defocusing case. On the left the conditional variace Vs|m shows a strong correlation between Pout and M. On the right we show the correlations between Pin and Pout Cs (dotted line) and
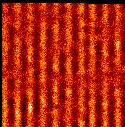
between Pin and M Cm (solid line) as well as the sum Cs+Cm (dashed line). QND measurements require Cs+Cm to be larger than 1, which is clearly fulfilled. On the right we show the near field (top) and far field (bottom) distribution of the output field fluctuations.
| We have studied the quantum correlations in a vectorial Kerr cavity
in the case in which, just above above the threshold of the spatial instabilitity,
the homogeneous pump gives rise to two tilted waves (M1 and M2) corresponding
to a stripe pattern in the near field.
We have shown the existence of anti-correlations between the quantum flutuations of the pump and the sum of intensities of M1 and M2. We have shown that in the self-defocusing case, where a vectorial pattern is formed it is possible to perform a Quantum Nondemolition measurement of the intensity fluctuations of the pump by using the fluctuations of M1 and M2 as “meter”. For the scalar pattern formed in the self-focusing case such a measurement does not fulfill the necessary conditions to be of nondemolition nature. M. Hoyuelos, A. Sinatra, P. Colet, L. Lugiato and M. San Miguel, Physical
Review A 59, 1622 (1999).
|
|
|
|