Living systems are very complicated supramolecular structures in which many of the factors responsible for the function of numerous biological processes are still poorly understood.  In some cases, much of the molecular complexity can  be ignored in a simplified view, and theoretical tools from the field of statistical mechanics and non-linear physics, as well as new computational methodologies, are being applied in the characterization of the structure and dynamics of biological systems. Still this field is in its infancy but already represents to the area of interdisciplinary physics a major challenge.

The sausage-string pattern, first noticed in the 1950s in laboratory animals, has been found in people who suffer from extremely high blood pressure and has remained a surgical mystery that has puzzled doctors for several decades. When a patient suffers high blood pressure, small blood vessels tend to alternately constrict and dilate along their length, forming a "sausage-string" pattern that is damaging to the patient.

In vivo micrograph of rat intestinal arterioles showing a typical “sausage-string” pattern following in an acute increase in blood pressure induced by intravenous infusion of angiotensin II.  (Taken from F. Gustafsson, Blood Pressure, 6, 71 (1997) , Published in Phys. Rev. Lett. 82, 1995 (1999) .

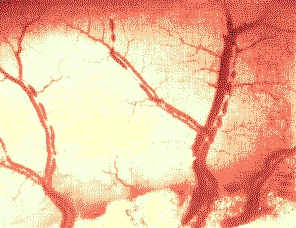We have proposed a new Rayleigh-type instability to explain the "sausage-string" pattern of alternating constrictions and dilatations formed in blood vessels under influence of a vasoconstricting agent. Our theory involves the nonlinear elasticity characteristics of the vessel wall, and provides predictions for the conditions under which the cylindrical form of a blood vessel becomes unstable. The theory also explains why similar patterns are not seen in larger blood vessels. This sort of knowledge could lead to ways to prevent the formation of the sausage-link shapes, which can disrupt blood flow, as for example, drugs that might change the elasticity of the arteries so that they don't become unstable under high pressure. (Reference: P. Alstrom, V. Eguíluz, M. Colding-Jorgensen, F. Gustafsson, N. Holstein-Rathlou, Phys. Rev. Lett. 82, 1995 (1999) ).

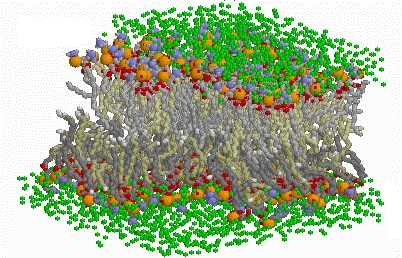
The lateral diffusion of lipids and proteins in cell membranes has been invoked in the description of many cellular processes, from directed transport in cellular locomotion to the functioning of molecules such as enzymes, ion pumps and receptors. It has been observed that the addition of small amounts of surfactant molecules in POPC bilayers causes the membrane to become  more rigid. This finding may indicate a possible control mechanism  of the fluidity and thus, the functionality of the membrane.

Schematic representation of a portion of a lipid bilayer composed of Phosphatidyl Cholines, generated with Rasmol. Taken from Heller et al. J. Chem Phys. 97, 8343 (93)

In order to gain more insight into the physical process underlying the lateral diffusion in lipid membranes, we have undertaken the study of the phenomenon using dynamic Monte Carlo techniques. To this end, we used an off-lattice approach in which the lipid chains are represented by a string of beads. The diffusion coefficient is found to follow the classical theory of Cohen and Turnbull at moderate  densities, but large deviations are found at low densities in  agreement with experimental studies. Our results indicate that at low densities, only small amplitude density fluctuations are needed to create sufficient free volume to induce lateral diffusion. In this regime, we found the diffusion to be entropically activated and governed by the chains "soft core" repulsion. Reference: T. Sintes, A. Baümgartner, Y. Levine,  Phys. Rev. E. 60, 814 (1999), J. Mol. Liq., 84, 77 (2000).

Fourier Spectrum and pitch complex tones

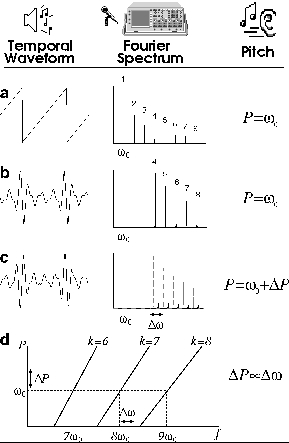
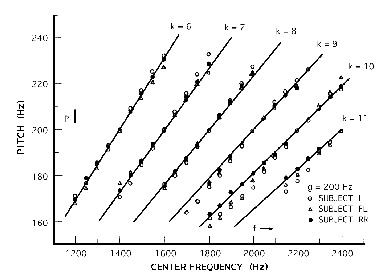
The sound of a note played on a musical instrument contains a variety of frequencies: the fundamental, which is usually the note that we perceive, as well as integer multiples of it called harmonics and responsible for the sound´s colour or timbre.  However, if we are exposed to a sound that only contains high harmonics and no fundamental, we nevertheless still hear the note corresponding to the fundamental. This is a well-known auditory phenomenon called “residue perception”. Understanding missing fundamental perception, as the phenomenon is also called, may be important not only for music but also for speech hearing since our ability to discern spoken words often relies on subtle features of the sound. We might think that intelligent hearing aids optimized to amplify or even reconstruct the fundamental frequency will do a better job than regular amplifiers.  Since the original attempts of Ohm and Seebeck last century, the issue of how perception of residues takes place remains largely open. One important controversial question is whether residual pitch is perceived after some level of neural processing in the primary auditory cortex or if it arises as a consequence of physical processes in the ear peripheral mechanisms.

Our theory relies mainly in the analysis of the so-called “pitch-shift effect” , and the results suggests that all that is really needed to explain most of the quantitative facts in residue perception is that the auditory system behaves as a nonlinear oscillator. We have shown that this shift coincides precisely with the expected response if the auditory mechanism were a nonlinear oscillator driven by a combination of periodic forces (generically resulting in a quasi periodic one) with the main spectral features of the sound to be perceived. Nonlinear oscillators driven by these kind of stimulii display a wide range of behaviour, ranging from a variety of resonant or synchronous responses to erratic and chaotic evolutions. When the components in the driving are those used to reveal the pitch-shift phenomenon, we can identify uniquely by a number theoretic argument, the largest subharmonic resonance involving the combination. In such resonant regime, the oscillator responds with the frequency that is related to, but not present amongst those in the driving signal. This frequency happens to fit without any parameter adjustment the experimental data on pitch-shift. Reference: J. Cartwright, D. González, O. Piro, Phys. Rev. Lett, 82, 5389 (1999).